Пример: Случайное блуждание

Моделирование случайного блуждания предоставляет иллюстрацию применения операций с массивами. Вначале рассмотрим случайное блуждание, начинающееся с \( 0 \) с шагами \( 1 \) и \( -1 \), происходящие с равной вероятностью.

Ниже представлен код сценария на чистом Python, который реализует простое случайное блуждание в 1000 шагов и использует модуль random:

import random

position = 0
walk = [position]
steps = 1000
for i in range(100):
    step = 1 if random.randint(0, 1) else -1
    position += step
    walk.append(position)

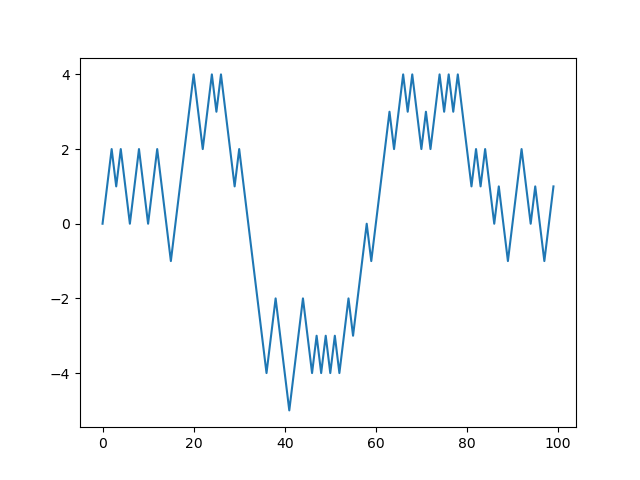
На рис. 3 графически представлены 100 первых значений одного случайного блуждания.

Заметим, что walk — это просто накопленная сумма случайных шагов, а она может быть вычислена с помощью метода массива. Таким образом, можно воспользоваться модулем np.random для генерации 1000 бросаний монеты за раз, установить соответствующие значения в \( 1 \) и \( -1 \) и вычислить накопленную сумму:

nsteps = 1000
draws = np.random.randint(0, 2, size=nsteps)
steps = np.where(draws > 0, 1, -1)

Отсюда можно получить статистические данные, такие, например, как минимум и максимум:

In [180]: walk.min()
Out[180]: -9

In [181]: walk.max()
Out[181]: 60

Более сложная статистика — время первого «перехода», т.е. шаг, на котором пусть достигает некоторого значения. Например, можно узнать, сколько времени понадобилось случайному блужданию, чтобы пройти как минимум 10 шагов от начала в любом направлении. Выражение np.abs(walk) >= 10 даст булев массив, указывающий, где элемент walk достиг или превысил значение \( 10 \). Но нам нужен индекс первого элемента, равного \( 10 \) или \( -10 \). Мы можем получить это с помощью функции argmax, которая вернет первый индекс максимального значения в булевом массиве (True — максимальное значение):

In [182]: (np.abs(walk) >= 10).argmax()
Out[182]: 297

Обратите внимание, что использование argmax здесь не всегда эффективно, потому что оно всегда выполняет полное сканирование массива. В этом особом случае, когда есть значение True, мы знаем, что это максимальное значение.

• ← Prev
• Next →