Первые шаги
Программа на Python с переменными
Рассмотрим пример иллюстрирующий математическую модель описывающий траекторию полета мяча в воздухе. Из второго закона Ньютона, предполагая незначительное сопротивление воздуха, мы можем вывести зависимость вертикального положения \( y \) мяча от времени \( t \): $$ \begin{equation*} \tag{1} y = v_0 t -0.5 g t^2 \end{equation*} $$ где \( v_0 \) — начальная скорость, \( g \) — ускорение свободного падения, значение которого положим равным \( 9.81 \) м/c \( ^2 \).
Сценарий
Рассмотрим сценарий на Python для вычисления по простой формуле. Предположим, что сценарий у нас сохранен в виде текста в файле ball.py
# -*- coding: utf-8 -*-
# Программа для вычисления положения мяча при вертикальном движении
v0 = 5 # Начальная скорость
g = 9.81 # Ускорение свободного падения
t = 0.6 # Время
y = v0*t - 0.5*g*t**2
Разбор сценария
Сценарий на языке Python — это текстовый файл (в нашем случае
ball.py), содержащий некоторые
инструкции. Мы можем читать сценарий и понимать, что программа
способна делать, но сам сценарий не выполняет никаких действий на
компьютере, пока интерпретатор Python не прочитает текст сценария и не
преобразует его в некоторые действия.
Когда сценарий запущен в интерпретаторе Python, он разбирается и выполняется
построчно. Первые две строки
являются # -*- coding: utf-8 -*-
# Программа для вычисления положения мяча при вертикальном движении
#,
интерпретатор Python воспринимает оставшуюся часть строки как
комментарий, пропускает ее и переходит к следующей строки.
Замечание
В первой строке указывается кодировка, в которой сохранен файл сценария (в нашем случае *— это UTF8). Если в сценарии не предполагается использование не ASCII символов, то первую строку можно опустить. Однако, мы можем использовать кириллический текст, поэтому в наших сценариях мы всегда будем указывать кодировку.
Следующие 3 строки, интерпретируемые Pyhton:
v0 = 5 # Начальная скорость
g = 9.81 # Ускорение свободного падения
t = 0.6 # Время
В Python выражения вида v0 = 5 известны как операторы
присваивания. Значение правой части, в нашем случае целое число
5, становится объектом, а имя переменной слева *— именованной
ссылкой на этот объект. Всякий раз, когда мы запишем v0, Python
заменит ее целым значением 5. Выражение v1 = v0 создает новое
имя для того же целого объекта со значением 5, а не копирует
объект.
Таким образом, прочитав эти строки интерпретатор Python знает три
переменных v0, g, t и их значения. Эти переменные используются
интерпретатором в следующей строке, фактически реализующей некоторую
формулу
y = v0*t - 0.5*g*t**2
В этой строке Python интерпретирует * как оператор умножения, - *---
вычитания, ** *— возведения в степень (естественно, + и \
интерпретируются как операторы сложения и деления соответственно). В
результате вычисляется значение по формуле в правой части выражения,
которое присваивается переменной с именем y. Последняя строка
сценария
print y
выводит на печать значение переменной y. Таким образом при запуске
сценария ball.by на экране будет выведено
число 1.2342. В тексте сценария имеются также и пустые строки, которые
пропускаются интерпретатором Python. Они добавлены для лучшей
читабельности кода.
Запуск сценариев Python
Сценарии Python обычно имеют расширение .py, но это не является
необходимым. Как мы уже говорили, рассмотренный выше сценарий сохранен
в файле ball.py. Запустить его можно
следующей командой:
python ball.py
Такая команда явно указывает, что в качестве интерпретатора файла
ball.py должен использоваться Python. Также могут задаваться
аргументы командной строки, который загружается сценарием.
Команда python ball.py ... должна запускаться в консольном окне
(терминал в Unix, Командная строка (Command Prompt) в MS Windows).
В случае, когда файлу установлено разрешение на выполнение (команда
chmod a+x ball.py) в ОС Unix (Linux), сценарий можно запускать
командой, сценарий можно запускать командой
./ball.py
В этом случае первая строка сценария должна содержать описание интерпретатора:
#!/usr/bin/env python
В ОС MS Windows можно писать просто
ball.py
вместо python ball.py, если расширение .py ассоциировано с
интерпретатором Python.
Программа на Python, использующая библиотечные функции
Представим, мы стоим на расстоянии, например, 10 м, и наблюдаете за тем как мяч поднимается в воздух после броска. Прямая соединяющая нас и мяч составляет некий угол с горизонтальной прямой, величина которого возрастает и убывает, когда мяч поднимается и опускается соответственно. Давайте рассмотрим положение мяча в некоторый момент времени, когда высота положения мяча равна 10 м.
Вычислим рассматриваемый нами угол. Перед тем как написать программу, мы должны сформулировать некий алгоритм, т.е. некий способ выполнения необходимых вычислений. В нашем случае, пусть \( x \) --- расстояние от нас до точки подброса мяча, а \( y \) — высота, на которой находится мяч. Таким образом, образуется угол \( \theta \) с поверхностью земли, где \( \mathrm{tg\,} \theta = y/x \). Следовательно, \( \theta=\mathrm{arctg\,}(y/x) \).
Напишем сценарий выполняющий эти вычисления. Введем переменные x и
y для координат положения \( x \) и \( y \), и переменную
angle для угла \( \theta \). Сценарий сохраним в файл
ball_angle.py
# -*- coding: utf-8 -*-
x = 10 # горизонтальное положение
y = 10 # вертикальное положение
angle = atan(y/x)
print (angle/pi)*180
В этом сценарии строка angle = atan(y/x) иллюстрирует
вызов функции atan, соответствующей математической функции
\( \mathrm{arctg} \), с выражением y/x в качестве аргумента
или входного параметра. Отметим, что тригонометрические функции
(такие как atan) возвращают значение угла в радианах, поэтому для
преобразования результата в градусы мы использовали выражение
(angle/pi)*180.
Теперь, запустив на выполнение сценарий, мы получим ошибку
NameError: name 'atan' is not defined
Очевидно, интерпретатор Python не распознал функцию atan, так как
эта функция еще не импортирована в программу. Достаточно большой
функционал доступен в интерпретаторе по умолчанию, однако намного
больший функционал реализован в библиотеках Python. Для того, чтобы
активировать использование дополнительного функционала, мы должны его
явно импортировать. В Python функция atan, как и множество других
математических функций, собраны в библиотеке math. Такая
библиотека в терминах Python называется модулем. Чтобы мы могли
использовать функцию atan в нашем сценарии, мы должны написать
from math import atan
Добавив данную строку в начало сценария и запустив его, мы приходим к
другой проблеме: переменная pi не определена. Переменная pi,
соответствующая значению \( \pi \), также определена в модуле math, и
тоже должна быть импортирована
from math import atan, pi
Очевидно, что достаточно сложно импортировать поименно все необходимые
нам функции и переменные из модуля math, поэтому существует
быстрый способ импортировать все из модуля math:
from math import *
Мы будем использовать такое выражение для импорта, чтобы иметь доступ ко всем общим математическим функциям. Таким образом рабочий сценарий ball_angle.py имеет вид:
# -*- coding: utf-8 -*-
from math import *
x = 10 # горизонтальное положение
y = 10 # вертикальное положение
angle = atan(y/x)
print (angle/pi)*180
На первый взгляд кажется громоздким использование библиотек, так как мы должны знать какой модуль импортировать, чтобы получить желаемый функционал. Возможно, более удобно иметь доступ ко всему необходимому в любое время. Однако это означает, что мы заполним память программы большим количеством информации, которую мы будем редко использовать для вычислений. Поэтому Python имеет большое количество библиотек, реализующих огромные возможности, из которых мы можем импортировать только необходимые в данный момент.
Программа на Python с векторизацией и построением графиков
Вернемся к задаче, описывающей вертикальное положение \( y \) мяча после подбрасывания. Предположим, что нас интересуют значения \( y \) в каждую миллисекунду первой секунды полета. Это требует повторения вычисления \( y = v_0 t - 0.5 g t^2 \) тысячу раз.
Также построим график зависимости \( y \) от \( t \) на отрезке \( [0, 1] \). Построение такого графика на компьютере подразумевает рисование прямых отрезков между точками кривой, поэтому нам понадобится много точек, чтобы создать визуальный эффект гладкой кривой. Тысячи точек, которые мы вычислим, нам будет достаточно для этого.
Реализацию таких вычислений и построения графика может быть реализовано следующим сценарием (ball_plot.py):
# -*- coding: utf-8 -*-
from numpy import linspace
import matplotlib.pyplot as plt
v0 = 5
g = 9.81
t = linspace(0, 1, 1001)
y = v0*t - 0.5*g*t**2
plt.plot(t, y)
plt.xlabel(u't (с)')
plt.ylabel(u'y (м)')
plt.show()
def height(t):
h = v0*t - 0.5*g*t**2
return h
h = lambda t: v0*t - 0.5*g*t**2
Замечание
В нашем сценарии для символьных аргументов мы использовали префикс
u (например, plt.xlabel(u't (с)')), чтобы указать, что
символы содержатся в кодировке UTF8.
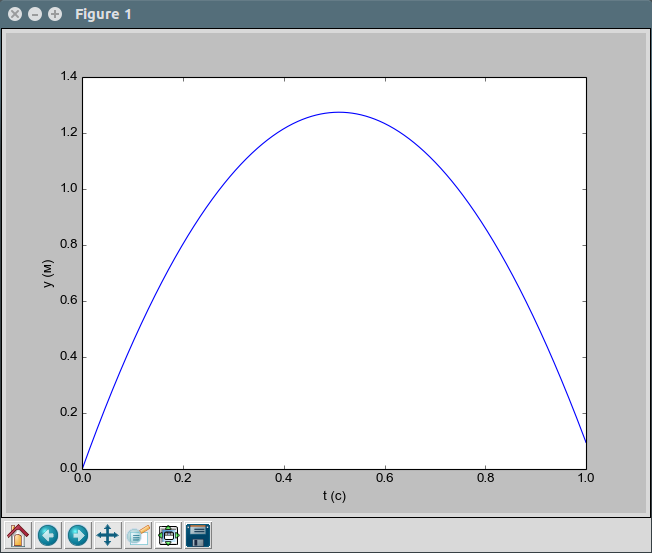
Данный сценарий строит график зависимости вертикального положения мяча
от времени (см. рис. :numref:`%s<1st-fig-1>`). Отметим, что строки для
вычисления из сценария ball.py из раздела
Программа на Python с переменными мало изменены, но значение y
вычисляется для тысячи точек.
Рассмотрим различия рассматриваемого сценария от предыдущих. Первое отличие это строки, которые могли выглядеть следующим образом:
from numpy import *
from matplotlib.pyplot import *
Мы видим, что numpy является модулем Python. Этот модуль содержит
огромный функционал для математических вычислений, а модуль
matplotlib.pyplot реализует возможности для построения двумерных
графиков. Приведенные выше строки представляют быстрый способ загрузки
всего функционала, связанного с вычислениями и построением
графиков. Однако, фактически мы используем только несколько функций в
нашем сценарии: linspace, plot, xlabel и
ylabel. Многие разработчики считают, что мы должны импортировать
только то, что нам нужно, а не весь возможный функционал:
from numpy import linspace
from matplotlib.pyplot import plot, xlabel, ylabel
Другие предлагают способ импорта, когда используется префикс для функций модуля
import numpy as np
import matplotlib.pyplot as plt
...
t = np.linspace(0, 1, 1001)
...
plt.plot(x,y)
Мы будем использовать все три способа. В нашем сценарии мы использовали два из них.
from numpy import linspace
import matplotlib.pyplot as plt
Рисунок 1: График, построенный с помощью нашего сценария.
Функция linspace принимает три аргумента и, в общем случае,
вызывается следующим образом:
linspace(start, stop, n)
Функция linspace генерирует n равноотстоящих координат,
начинающихся со значения start, и заканчивающихся
stop. Выражение linspace(0, 1, 1001) создает 1001 координату
от 0 до 1 включительно. Математически это означает, что отрезок
\( [0,1] \) разбивается на 1000 равных отрезков и значения координат
в этом случае вычисляются следующим образом: \( t_i = i/1000,\ i = 0, 1,
\ldots, 1000 \).
Функция linspace возвращает объект класса array,
т.е. некоторый набор чисел (массив). При выполнении арифметических операций с
такими объектами, на самом деле эти операции осуществляются для каждого
элемента массива. В результате получается аналогичный массив из 1001
элемента, который сохраняется в переменную y. Таким образом y
также является массивом.
Такой подход вычисления нескольких чисел в одну строку называется
векторизацией. Этот способ очень удобен, так как сокращает не только
количество кода, но и время вычислений по сравнению с использованием
циклов for или while.
Команды для построения графиков достаточно просты:
1. plot(x, y) означает построение графика зависимости y от
x
2. xlabel(u't (с)') помещает текст t (с) на оси x.
3. ylabel(u'y (м)') помещает текст y (м) на оси y.
Некоторые основные понятия
Мы рассмотрели несколько простых примеров, иллюстрирующих использование Python для решения простейших математических задач. Прежде чем мы перейдем к более сложным и достаточно реалистичным примерам, рассмотрим некоторые понятия, которые будут часто использоваться в следующих главах: переменные, объекты. Кроме того рассмотрим такие понятия, как ошибки округления, приоритет арифметических операций, деление целых чисел. Также получим чуть больше информации о функционале Python при работе с массивами, построении графиков и выводе результатов.
Интерактивное использование Python
Python можно использовать интерактивно, т.е. мы можем не писать
сначала сценарий и запускать его, выполнять операторы и выражения в
оболочке Python. Мы рекомендуем использовать оболочку IPython (на
наш взгляд --- лучшая из альтернативных оболочек Python). При
использовании IDE Spyder, IPython доступен при запуске в правом
нижнем окне. Следуя подсказке IPython In [1]: (подсказка *— это
так называемый знак готовности, т.е. программа предлагает вводить
команды), мы можем выполнять вычисления
In [1]: 2+2
Out[1]: 4
In [2]: 2*4
Out[2]: 8
In [3]: 10/2
Out[3]: 5
In [4]: 4**4
Out[4]: 256
Ответу интерпретатора IPython предшествует Out [q]:, где q *---
номер соответствующей входной строки.
Заметим, что, как и в сценарии, можно выполнить команду
from math import * для использования, например, pi или
математических функций. Также можно импортировать и другие модули,
когда они понадобятся.
Можно также определять переменные и использовать формулы интерактивно:
In [1]: v0 = 5
In [2]: g = 9.81
In [3]: t = 0.6
In [4]: y = v0*t - 0.5*g*t**2
In [5]: print y
1.2342
Иногда может понадобиться повторить команду, которую уже выполняли ранее. Для этого можно воспользоваться стрелкой вверх на клавиатуре. Нажав эту клавишу один получим предыдущую команду, два раза *— команду перед этой и т.д. С помощью стрелки вниз мы будем пробегать вперед по истории команд. Также можно поправить выбранную команду перед ее выполнением.
Арифметические операции, круглые скобки и ошибки округления
Как известно арифметические операции +, -, *, / и
** имеют приоритет выполнения. Python обрабатывает операции слева
направо, вычисляя один операнд (часть выражения между двумя
последовательными + или -). Внутри каждого операнда операция
** выполняется перед * или /. Рассмотрим выражение
x = 2*4**3 + 10*2 - 1.0/4. В нем три операнда, и Python
начинает обрабатывать их слева. В первом операнде 2*4**3
интерпретатор сначала вычислит 4**3, что даст 64, затем
результат умножается на 2. Получаем 128. Следующий операнд
10*2, т.е. 20. Затем два операнда складываются, что дает
148. Результат вычисления последнего операнда равен
0.25. Таким образом значение переменной x становится равным
147.75.
Отметим, что круглые скобки используются для группировки
операндов. Пусть x = 4 получим результат деления числа 1.0 на
x+1. Приведем варианты записи в интерпретаторе Python:
In [1]: 1.0/x+1
Out[1]: 1.25
In [2]: 1.0/(x+1)
Out[2]: 0.2
При первой попытке выполнено сначала деление 1.0 на x, к
которому затем прибавляется 1. Python не воспринимает x+1 как
знаменатель. Во второй попытке мы воспользовались круглыми скобками,
чтобы сгруппировать знаменатель. Так как большинство чисел в памяти
компьютера могут быть представлены только приближенно, иногда может
получаться не точное значение, что обусловлено ошибками округления.
Переменные и объекты
Переменные в Python имеют некоторый тип. Если мы запишем x = 2 в
сценарии Python, то x становится целой переменной, т.е. переменной
типа int (целое число). Аналогично, выражение x = 2.0 означает, что x
переменная типа float (действительное число). В любом случае, Python
воспринимает x как объект типа int или float. Узнать тип
объекта x можно с помощью команды type(x). Еще один основной
тип переменной *— это тип str или строка, используемый для
текстовых объектов. Такие переменные задаются двойными или одинарными
кавычками:
x = "This is the text"
y = 'This is the text'
Оба оператора создают объекты типа str.
При необходимости можно преобразовывать типы. Если, например, x
--- объект типа int, с помощью выражения y = float(x) мы
создаем объект с плавающей точкой. Аналогично можно получить целое
число из типа float, воспользовавшись int(x). Преобразование
типов может осуществлятся автоматически, как будет показано чуть ниже.
Договоримся, что имена переменных должны быть информативными. При
вычислении математических величин, которые имеют стандартные символы,
например, \( \alpha \), это следует отразить в имени переменной,
используя слово alpha в имени переменной в сценарии. Если,
например, вычисляем число овец (sheep), то одним из подходящих имен
для переменной может быть no_of_sheep. Такие имена переменных
делают более читабельным код программы. Имена переменных могут
содержать цифры и знак подчеркивания, но не могут начинаться с
цифры. Буквы могут быть строчными и прописными, в Python они
отличаются. Отметим, что некоторые имена в Python зарезервированы и мы
не можем их использовать в качестве имен переменных. Вот некоторые
примеры: for, while, else, global, return и
elif. Если мы случайно используем зарезервированное слово в
качестве имени переменных, то получим сообщение об ошибке.
Выражение x = 2 присваивает значение 2 переменной x. Как
можно увеличить x на 4? Мы можем воспользоваться выражением
x = x + 4 или выражением (дающим более быстрые вычисления)
x += 4. Аналогично, x -= 4 уменьшает значение переменной x
на 4, x *= 4 умножает x на 4, x /= 4 делит x на 4,
обновляя значение переменной x.
Что произойдет, если x = 2, т.е. объект типа int, и мы к нему
прибавим 4.0 (объект типа float)? Будет иметь место
автоматическое преобразование типов и новое x примет значение
6.0, т.е. станет объектом типа float.
In [1]: x = 2
In [2]: type(x)
Out[2]: int
In [3]: x = x +4.0
In [4]: x
Out[4]: 6.0
In [5]: type(x)
Out[5]: float
Целочисленное деление
Следует обратить внимание на еще одну проблему — целочисленное деление*. Рассмотрим пример деления числа 1 на 4:
In [1]: 1/4
Out[1]: 0
In [2]: 1.0/4
Out[2]: 0.25
Представлены два способа выполнения этой операции, при этом второй вариант дает правильный результат.
В Python версии 2 первый вариант дает результат так называемого
целочисленного деления. В этом случае все десятичные знаки
отбрасываются, т.е. результат округляется до ближайшего меньшего
целого числа. Чтобы избежать этого мы можем явно указать десятичную
точку либо в числителе, либо в знаменателе, либо в обоих
операндах. Если числитель или знаменатель являются переменными,
т.е. мы вычисляем выражение 1/x, то, чтобы получить результат типа
float, можно записать 1/float(x).
В Python версии 3 операция / дает результат типа float, а для
целочисленного деления используется только операция // (//
есть в Python версии 2).
Форматированный вывод текста и чисел
В результате научных вычислений часто на печать выводится текст,
содержащий числа. Естественно желание контролировать формат вывода
числа. Например, мы хотим вывести число 1/3 как 0.33 или в
виде 3.3333e-1 (\( 3.3333 \times 10^{-1} \)). Команда print
--- основной инструмент для вывода текста и чисел, обеспечивающий
полное управление форматированием. Первый аргумент команды print
--- это строка с определенным синтаксисом, задающим формат вывода, так
называемый printf-синтаксис. Такое название происходит от функции
printf из языка программирования C, где такой синтаксис был введен
впервые.
Предположим, мы имеем действительное число \( 12.39486 \), целое число \( 23 \), и текст «сообщение», которые мы хотим вывести на печать двумя способами:
real=12.394, integer=23, string=сообщение
real=1.239e+01, integer= 23, string=сообщение
В первом варианте действительное число выведено в десятичной записи 12.394, а
во втором в научной записи (с плавающей точкой) 1.239e+01. Целое
число в первом варианте выведено в компактном виде, а во втором
варианте в текстовом поле из четырех символов.
Следующий сценарий
(formatted_print.py) использует
printf-синтаксис для управления форматированным выводом:
# -*- coding: utf-8 -*-
real = 12.29486
integer = 23
string = 'сообщение'
print "real=%.3f, integer=%d, string=%s" % (real, integer, string)
print "real=%4.3e, integer=%3d, string=%s" % (real, integer, string)
Вывод команды print --- это строка, содержащая текст и набор
переменных, вставляемых в текст в местах отмеченных символом
%. После % идет определение формата, например %f (для
действительных чисел), %d (для целых чисел) или %s (для
строк). Формат вида %4.3f означает, что действительное число
выводится в десятичной записи, с тремя знаками после запятой, в поле
из 4 символов. Вариант .3f означает вывод числа в наименьшем
возможном поле, в десятичной записи, с тремя знаками после
запятой. Замена f на e или E приводит к выводу в научном
формате: 1.239e+01 или 1.239E+01. Запись %4d означает
вывод целого числа в текстовом поле из четырех
символов. Действительные числа также могут выводится форматом %g,
который используется для автоматического выбора между десятичным и
научным форматом, дающим более компактную запись (научный формат
удобен для очень маленьких и очень больших чисел).
Типичный пример, когда требуется printf-синтаксис для вывода, когда нужно напечатать выровненные колонки. Предположим мы хотим напечатать колонку значений \( t \) и колонку с соответствующими значениями функции \( f(t) = t\sin t \). Простейший вариант
# -*- coding: utf-8 -*-
from math import sin
t = 0
dt = 0.55
t += dt; f = t*sin(t)
print t, f
t += dt; f = t*sin(t)
print t, f
t += dt; f = t*sin(t)
print t, f
дает следующий результат
Terminal> python2 src-python/unformatted_print.py
0.55 0.287477975912
1.1 0.980328096068
1.65 1.64482729695
Обратите внимание на то, что колонки не выровнены, что дает
нечитабельный вывод. Добавив в функцию print следующий аргумент
'%6.2f %8.3f' %(t, f), мы управляем шириной каждой колонки и
количеством знаков после запятой:
0.55 0.287
1.10 0.980
1.65 1.645
Современная альтернатива printf-синтаксису
В современном Python отдается предпочтение использованию метода
format. Например
print 'При t = {t:g} с, y = {y:.2f} м'.format(t=t, y=y)
соответствует следующему printf-синтаксису:
print 'При t = %g с, y = %.2f м' % (t, y)
Область, куда помещается значение переменной, теперь задается
фигурными скобками, а в методе format перечисляем имена
переменных внутри фигурных скобок и соответствующие им имена
переменных в программе.
Так как printf-синтаксис широко распространен в во многих языках
программирования, мы будем использовать его. Однако уже во многих
программах на Python вы можете встретить новый способ
форматирования вывода, поэтому мы привели его здесь.
Массивы
В сценарии ball_plot.py из раздела Программа на Python с векторизацией и построением графиков мы использовали массивы NumPy. Такие массивы создаются и обрабатываются в соответствии с некоторыми правилами, при этом управлять массивами можно как целиком, так и отдельными элементами массива.
Рассмотрим такой пример: предположим у нас есть данные о росте четырех
человек. Эти данные мы можем сохранить в массиве с именем h
следующим образом:
h = zeros(4)
h[0] = 1.60
h[1] = 1.75
h[2] = 1.82
h[3] = 1.72
Здесь элементами массива являются h[0], h[1] и т.д. Самая
первая строка в приведенном фрагменте кода
h = zeros(4)
дает указание Python зарезервировать, или выделить, пространство в
памяти для массива h из четырех элементов с начальными значениями
равными 0. Следующие четыре строки заменяют нулевые значения элементов
массива заданными. Элементы, как правило, индексируются с 0.
Используя двоеточие, мы можем получать срез массива. Например, чтобы
создать новый массив из двух элементов h[1] и h[2], мы можем
использовать следующую конструкцию slice_h = h[1:3]. Отметим, что
определение 1:3 означает индексы 1 и 2, т.е. последний
индекс в определении среза не включается. Полученный массив
slice_h, индексируется стандартно с 0. Доступ к самому последнему элементу
массива можно получить следующим образом h[-1].
Копирование массива требует осторожности, так как запись new_h =
h означает присваивание ссылки, т.е. в этом случае, когда мы будем
изменять значения элементов массива h, будут изменяться значения
соответствующих элементов массива new_h.
Построение графиков
Иногда нам нужно построить графики двух функций на одном
рисунке. Предположим у нас есть массив h, заданный выше и массив
H. График с двумя кривыми можно построить следующим образом
(сценарий plotting_two.py):
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
h = np.zeros(4)
h[0] = 1.60; h[1] = 1.75; h[2] = 1.82; h[3] = 1.72
H = np.zeros(4)
H[0] = 0.60; H[1] = 0.30; H[2] = 1.90; H[3] = 1.99
numbers = np.zeros(4)
numbers[0] = 1; numbers[1] = 2; numbers[2] = 3; numbers[3] = 4
plt.plot(numbers, h, numbers, H)
plt.xlabel(u'Номер по порядку')
plt.ylabel(u'Значение')
plt.show()
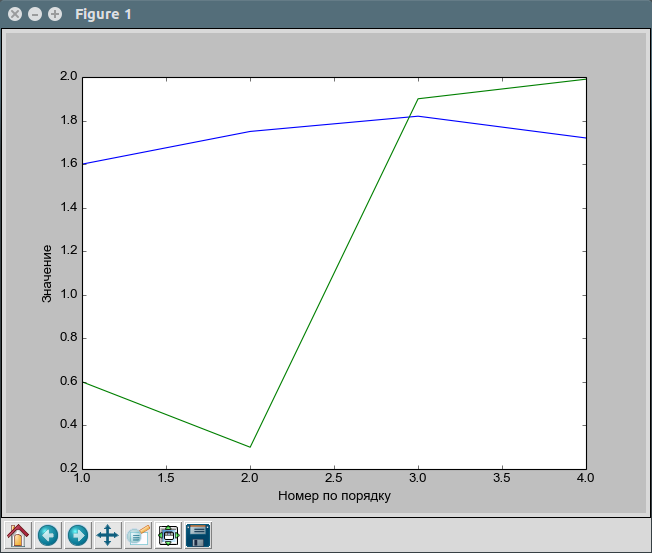
Результат работы сценария представлен на рисунке
Рисунок 2: График, построенный с помощью сценария.
Две кривые на одном графике можно построить и другим способом,
используя две команды plot. Например, вы можете построить первую
кривую
plot(numbers, h)
hold('on')
Затем можно выполнить различные команды и вычисления в сценарии перед построением второй кривой
plot(numbers, H)
hold('off')
Мы здесь использовали функцию hold: hold('on') сообщает
Python, чтобы следующие кривые строились в том же окне. Python
выполняет это до тех пор пока не появится команда
hold('off'). Если не использовать команды hold('on') и
hold('off'), то вторая команда построения кривой перепишет первую,
т.е. появится только вторая кривая.
В случае, когда необходимо построить две кривые на отдельных графиках можно построить стандартно первую кривую
plot(numbers, h)
затем выполнить следующие команды
figure()
plot(numbers, H)
Стандартно Python при построении графиков рисует прямые отрезки между точками со значениями. Можно также организовать другие способы вывода. Например, команда
plot(h, '*')
построит только точки значений отмеченные символом * (можно
использовать также другие символы).
Кроме того, Python позволяет добавлять дополнительную информацию на графики. Например, можно добавить легенду с помощью следующей команды
legend('hH')
или название графика
title('График')
Команда
axis([xmin, xmax, ymin, ymax])
задает область построения графика: для оси \( x \) участок от
xmin до xmax, для оси \( y \) участок от
ymin до ymax
Сохранение графика в фалы соответствующих форматов можно выполнить с помощью следующих команд:
savefig('pic.png')
savefig('pic.jpg')
savefig('pic.gif')
savefig('pic.eps')
savefig('pic.pdf')
Матрицы
Для линейной алгебры могут понадобится стандартные операции, например, умножение матрицы на вектор. Для этого можно использовать специальный тип. Например, мы хотим вычислить вектор \( \mathbf{y} \) следующим образом \( \mathbf{y} = \mathbf{A}\mathbf{x} \), где \( \mathbf{A} \) --- матрица размера \( 2\times 2 \), \( \mathbf{x} \) --- вектор. Это можно реализовать следующим образом (сценарий mat_vec_mult.py)
# -*- coding: utf-8 -*-
from numpy import zeros, mat, transpose
x = zeros(2)
x = mat(x)
x = transpose(x)
x[0] = 1.0; x[1] = 3.0
A = zeros((2,2))
A = mat(A)
A[0,0] = 1.0; A[0,1] = 2.0
A[1,0] = 3.0; A[1,1] = 4.0
y = A*x
print y
Здесь сначала x создан как объект типа array, затем тип
переменной x преобразован в тип matrix с помощью команды
mat(x). Далее матрица-строка x преобразована в матрицу столбец
с помощью операции транспонирования transpose(x). Создана матрица
A как массив размерности \( 2\times 2 \) командой
zeros((2,2)), преобразована в тип matrix. Затем заданы значения
каждому элементу матрицы. И наконец, умножение матрицы на вектор
выполнено операцией y=A*x. Запуск сценария дает
[[ 7.]
[ 15.]]
Входные данные
Как известно для выполнения вычислений компьютерным программам необходимы входные данные. В предыдущих примерах мы определяли входные данные как переменные, задавая их значения в самой программе. Однако очень часто удобно вводить данные во время выполнения программы посредством диалога с пользователем. Ниже приведен пример, где сценарий задает вопрос, а пользователь должен ввести данные.
# -*- coding: utf-8 -*-
age = input('Введите Ваш возраст\n')
print u'Вы на половине пути к %d' % (age*2)
После запуска сценария первая строка определяет переменную age и
устанавливает ей значение, введенное пользователем. Вторая строка
объединяет вычисление и вывод результата на экран.
Функция input удобна для вводя чисел, списков и кортежей. Для
ввода строковых переменных пользователь должен заключать в кавычки
вводимые данные, либо можно воспользоваться функцией raw_input:
name = raw_input('Введите Ваше имя: ')
Конечно, существуют другие способы ввода входных данных, например, графический интерфейс пользователя, параметры командной строки или чтение входных данных из файла.
Символьные вычисления
Несмотря на то, что наш курс посвящен в основном численным методам, возникнут ситуации, когда будут полезны символьные (точные или аналитические) вычисления. Выполнение символьных вычислений означает, что мы осуществляем вычисления с символами, а не с числовыми значениями. Проиллюстрируем отличие символьных вычислений от численных на небольшом примере. Численные расчеты могут быть следующими
x = 2
y = 3
z = x*y
print z
В результате на экране мы получим число 6. Символьная версия приведенного кода может быть следующей
from sympy import *
x, y = symbols('x y')
z = x*y
print z
Этот код дает символьный результат x*y. Отметим, что в этом случае
не задаются числовые значения символьным переменным, а используются
только символы.
Выполнение символьных вычислений в Python обеспечивает пакет
SymPy. Каждый символ представлен переменной, но имя символа должно
быть определено либо командой Symbol(имя) для одного символа, либо
командой symbols(имя1 имя2 ...) для нескольких символов. В
сценарии symbolic.py
# -*- coding: utf-8 -*-
from sympy import *
x = Symbol('x')
y = Symbol('y')
print x**2 + 3*y**3
print diff(x**3, x) # дифференцирование
print integrate(tan(x), x) # интегрирование
print simplify((x**2+x**3)/x**2) # упрощение выражения
print limit((1+x)**(1/x), x, 0) # вычисление предела
print solve(x**2-16, x) # решение уравнения x^2=16
Также доступны другие символьные вычисления: разложение в ряд Тейлора, линейная алгебра (операции с матрицами и векторами), решение некоторых дифференциальных уравнений и т.д.
Удаление не используемых данных
Python имеет автоматический сборщик мусора. Это означает, что нет необходимости удалять переменные (или объекты), которые больше не используются. Python заботится об этом сам. Это отличает его от, например, Matlab, где иногда требуется явно удалять переменные.
Совет
Если выражение в программе слишком длинное, его можно продолжить на следующей строке вставкой обратной косой черты перед переходом на новую строку. Однако, не должно быть пробелов после обратной косой черты.